AQUI PUEDEN OBSERVAR EL DISEÑO PRELIMINAR DEL SOFTWARE MATH FOR KIDS
ESPERAMOS LES GUSTE!!!!
MATH FOR KIDS
jueves, 11 de noviembre de 2010
FORMULAS PARA RECORDAR
a + b = a + b Suma de Fracciones homogéneas
c c c
a + b = ad + bc Suma de Fracciones heterogéneas
c d cd
a - b = a - b Resta de Fracciones homogéneas
c c c
a - b = ad - bc Resta de Fracciones heterogéneas
c d cd
a · b = ab Multiplicación de Fracciones
c d cd
a ÷ b = a · d = ad División de Fracciones
c d c b cb
OPERACIONES ENTRE FRACCIONARIOS
OPERACIONES ENTRE FRACCIONARIOS
MULTIPLICACION
 Es muy sencillo. Para multiplicar dos o más fracciones, se multiplican "en línea". Esto es, el numerador por el numerador y el denominador por el denominador.
Es muy sencillo. Para multiplicar dos o más fracciones, se multiplican "en línea". Esto es, el numerador por el numerador y el denominador por el denominador.
DIVISION
MULTIPLICACION
MULTIPLICACIÓN DE UNA FRACCIÓN POR UNA FRACCIÓN |
Ejemplo:
3 | 7 | 3x7 | 21 | |||
---- | x | ---- | = | ------- | = | --- |
2 | 4 | 2x4 | 8 |
DIVISION
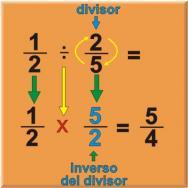
| Para dividir dos fracciones usamos el siguiente procedimiento: Invertimos el divisor (segunda fracción); al hacer esto nuestra división se convierte en una multiplicación. Observa el siguiente ejemplo: Dividir 1/2 : 1/5 Recuerda: El inverso de un entero es igual a una fracción con numerador igual a 1 Ejemplo: |
OPERACIONES ENTRE FRACCIONARIOS
OPERACIONES ENTRE FRACCIONARIOS
SUMA
 Primer caso: la suma de dos ó más fracciones que tienen el mismo denominador es muy sencilla, sólo hay que sumar los numeradores y se deja el denominador común. Ejemplo:
Primer caso: la suma de dos ó más fracciones que tienen el mismo denominador es muy sencilla, sólo hay que sumar los numeradores y se deja el denominador común. Ejemplo:
 Segundo caso: la suma de dos o más fracciones con distinto denominador es un poco menos sencilla. Vamos paso a paso:
Segundo caso: la suma de dos o más fracciones con distinto denominador es un poco menos sencilla. Vamos paso a paso:

RESTA
Tenemos dos casos:
 Primer caso: la resta de dos ó más fracciones que tienen el mismo denominador es muy sencilla, sólo hay que restar los numeradores y se deja el denominador común. Ejemplo:
Primer caso: la resta de dos ó más fracciones que tienen el mismo denominador es muy sencilla, sólo hay que restar los numeradores y se deja el denominador común. Ejemplo:
 Segundo caso: la resta de dos o más fracciones con distinto denominador es un poco menos sencilla. Vamos paso a paso:
Segundo caso: la resta de dos o más fracciones con distinto denominador es un poco menos sencilla. Vamos paso a paso:
como los denominadores son idénticos podemos restarla como en el caso 1.
4º Resta:
SUMA
Tenemos dos casos:
- Fracciones que tienen el mismo denominador;
- Fracciones que tienen el distinto denominador
4 | 2 | 6 | ||
---- | + | ---- | = | --- |
5 | 5 | 5 |
1º. Se haya el mínimo común múltiplo de los dos denominadores
2º Se calcula el numerador con la fórmula: numerador antiguo x denominador común y dividido por denominador antiguo
3º Se procede como en el primer caso (dado que las fracciones tienen el mimos denominador)
Ejemplo:
3 | 4 |
---- | ---- |
4 | 2 |
1º Calculamos el mínimo común múltiplo (m. c. m.) el m.c.m. (4, 2) = 4.
2º Calculamos los numeradores.
Numerador de la primera fracción: 3 x 4 : 4 = 3
Numerador de la segunda fracción: 4 x 4 : 2 = 8
Numerador de la segunda fracción: 4 x 4 : 2 = 8
3º Tenemos pues una fracción que es:
3 | 8 |
---- | ---- |
4 | 4 |
como los denominadores son idénticos podemos sumarla como en el caso 1.
4º Suma:
3 | 8 | 11 | ||
---- | + | ---- | = | --- |
4 | 4 | 4 |

RESTA
Tenemos dos casos:
- fracciones que tienen el mismo denominador;
- fracciones que tienen el distinto denominador
7 | 2 | 5 | ||
---- | - | ---- | = | --- |
9 | 9 | 9 |
Ejemplo:1º. Se haya el mínimo común múltiplo de los dos denominadores
2º Se calcula el numerador con la fórmula: numerador antiguo x denominador común y dividido por denominador antiguo
3º Se procede como en el primer caso (dado que las fracciones tienen el mismo denominador)
6 | 1 |
---- | ---- |
4 | 2 |
1º Calculamos el mínimo común múltiplo (m. c. m.) el m.c.m. (4, 2) = 4.
2º Calculamos los numeradores.
Numerador de la primera fracción: 6 x 4 : 4 = 6
Numerador de la segunda fracción: 1 x 4 : 2 = 2
Numerador de la segunda fracción: 1 x 4 : 2 = 2
3º Tenemos pues una fracción que es:
6 | 2 |
---- | ---- |
4 | 4 |
4º Resta:
6 | 2 | 4 | ||
---- | - | ---- | = | --- |
4 | 4 | 4 |
jueves, 4 de noviembre de 2010
RECOMENDACIONES
A CONTINUACIÓN LES DEJO ALGUNOS LINKS Y VÍDEOS QUE PUEDEN AYUDARLOS EN LA COMPRENSIÓN DEL ESTE TEMA DE FRACCIONARIOS, RECUERDEN LO MAS IMPORTANTE PARA APRENDER ES PRACTICAR
BUENA SUERTE!!!!!!!!!!!!!!!
LINKS DE AYUDA:
http://www.profesorenlinea.cl/cursos/3matematicas.html
http://matematicastercerciclo.blogspot.com/2010_01_01_archive.html
http://www.slideshare.net/albeiromendoza/fraccionarios-1057278
http://www.cespro.com/Materias/MatContenidos/ContMatematicas/Matematicas_Basicas1.htm
http://www.youtube.com/watch?v=xjhUEOPJx7A&feature=related
FRACCIONES - AMPLIFICACION Y SIMPLIFICACION
AMPLIFICACIÓN Y SIMPLIFICACIÓN DE FRACCIONES
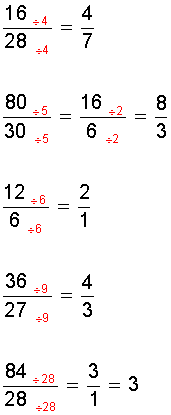
SIMPLIFICACIÓN
AMPLIFICACIÓN
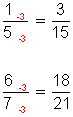
SIMPLIFICACIÓN
Si el numerador y el denominador de una fracción son divisibles por un mismo número, d, distinto de 1 o -1, al dividirlos por d se obtiene otra fracción equivalente a ella. Se dice que la fracción se ha simplificado o se ha reducido.
Simplificar una fracción significa dividir por un mismo número tanto el numerador como el denominador, para que la fracción (mostrada ahora con números distintos pero menores) mantenga su proporcionalidad (que su valor se mantenga).
Sólo se podrán simplificar fracciones cuando el numerador y denominador sean divisibles por un número común.
Cada vez que se simplifique una fracción se debe llegar hasta la fracción irreductible, es decir, aquella fracción que no se puede simplificar más (achicar más).
Ejemplos:

Esta operación, después de ejercitarla y dominarla, normalmente se hace en forma rápida, directa y hasta intuitivamente. Pero para empezar a dominarla debemos considerar los siguientes pasos previos:
Microsoft ® Encarta ® 2009. © 1993-2008 Microsoft Corporation. Reservados . todos los derechos.
AMPLIFICACIÓN
Es multiplicar el denominador y numerador de una fracción por un mismo número. Este número permite que la fracción aumente de valor tantas veces como veces se amplifica.
Por ejemplo, si la fracción se amplifica por dos, significa que aumentará su valor al doble.
Siempre que se amplifique una fracción se obtendrán fracciones equivalentes; es decir, fracciones que representan la misma cantidad.
Ejemplos:
Fracciones amplificadas por 3.
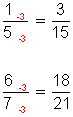
Tomado de :
FRACCIONARIOS - CONCEPTOS BASICOS
HOLA A TODOS A CONTINUACIÓN VAMOS A DESARROLLAR PARTE DE LA TEORÍA PROPUESTA PARA EL DESARROLLO DE ESTE BLOG: FRACCIONARIOS, ADJUNTAREMOS LA INFORMACIÓN NECESARIA Y NOS AYUDAREMOS DE ALGUNOS RECURSOS DE LA WEB 2.0
ESPERAMOS LES SEA ÚTIL!!!!!!!!!!!!!!!
FRACCIONARIOS
1.¿¿¿¿¿ QUE ES UN FRACCIONARIO?????
Un a fraccion es el cociente indicado __a__ de dos números enteros que se llaman
b
numerador, a, y denominador, b. Ha de ser b ≠ 0. Los fraccionarios son aquellos que representan una o mas partes de la unidad.
El denominador indica las partes en que se divide la fracción, y el numerador indica la cantidad que tomamos.
Si el numerador es múltiplo del denominador, la fracción representa a un número entero.
ESPERAMOS LES SEA ÚTIL!!!!!!!!!!!!!!!
FRACCIONARIOS
1.¿¿¿¿¿ QUE ES UN FRACCIONARIO?????
Un a fraccion es el cociente indicado __a__ de dos números enteros que se llaman
b
numerador, a, y denominador, b. Ha de ser b ≠ 0. Los fraccionarios son aquellos que representan una o mas partes de la unidad.
El denominador indica las partes en que se divide la fracción, y el numerador indica la cantidad que tomamos.
Si el numerador es múltiplo del denominador, la fracción representa a un número entero.
Si el numerador no es múltiplo del denominador, la fracción representa a un número fraccionario, es decir, a un número no entero.
EJEMPLOS:
125 > numerador Esta fracción representa un
______ = 25 numero exacto, ya que el nume-
rador es múltiplo del denomina-
5 > denominador dor.
Los fraccionarios pueden ser representados de diferentes maneras, ya sea gráficamente, numéricamente o por medio de la recta numérica ;
Tomado de :
Microsoft ® Encarta ® 2009. © 1993-2008 Microsoft Corporation. Reservados todos los derechos.

EJEMPLOS:
125 > numerador Esta fracción representa un
______ = 25 numero exacto, ya que el nume-
rador es múltiplo del denomina-
5 > denominador dor.
Los fraccionarios pueden ser representados de diferentes maneras, ya sea gráficamente, numéricamente o por medio de la recta numérica ;
Tomado de :
Microsoft ® Encarta ® 2009. © 1993-2008 Microsoft Corporation. Reservados todos los derechos.
 |
| http://secretariado.wordpress.com/2009/08/07/numeros-fraccionarios/ |

PARTES DE UN NÚMERO FRACCIONARIO
Una fracción propia esta formada por un Númerador y un Dénominador de manera que:
6 9
_______ , ______
8 15
En cambio una fracción impropia es aquella en la cual el Númerador es mayor que el Dénominador, es decir:
9 23
_______ , _________
5 12
En el caso de una fracción impropia, esta se puede representar de forma puramente fraccional o de forma mixta, es decir con una parte entera.
Suscribirse a:
Comentarios (Atom)